Algorithms

SwarmMakie aims to offer several beeswarm algorithms, which give different results. You can change the algorithm which SwarmMakie uses by passing it as a keyword argument algorithm, or mutating plot.algorithm after the fact.

Currently, it offers the SimpleBeeswarm and WilkinsonBeeswarm algorithms, which are inspired by Matplotlib and Leland Wilkinson's original paper respectively, and a no-op NoBeeswarm algorithm which simply decomposes back to the original data.

In addition, SwarmMakie offers jittered scatter plots as algorithms to beeswarm. These aren't exactly beeswarm plots since they don't guarantee that all points are non-overlapping, but they can still be useful to show distributions, especially for larger numbers of points where all points cannot fit into a beeswarm. These algorithms are accessible as UniformJitter, PseudorandomJitter, and QuasirandomJitter, similar to ggbeeswarm's options.

Overview

Here's an overview of all the available algorithms. Each of the built-in algorithms can be accessed with a Symbol as a shorthand.

using SwarmMakie, CairoMakie

algorithms = [:default, :wilkinson, :none, :uniform, :pseudorandom, :quasirandom]
fig = Figure(; size = (800, 450))
xs = rand(1:3, 400); ys = randn(400)

for (i, algorithm) in enumerate(algorithms)
    beeswarm(
        fig[fldmod1(i, 3)...], xs, ys;
        color = xs, algorithm, markersize = 4,
        axis = (; title = repr(algorithm))
    )
end

fig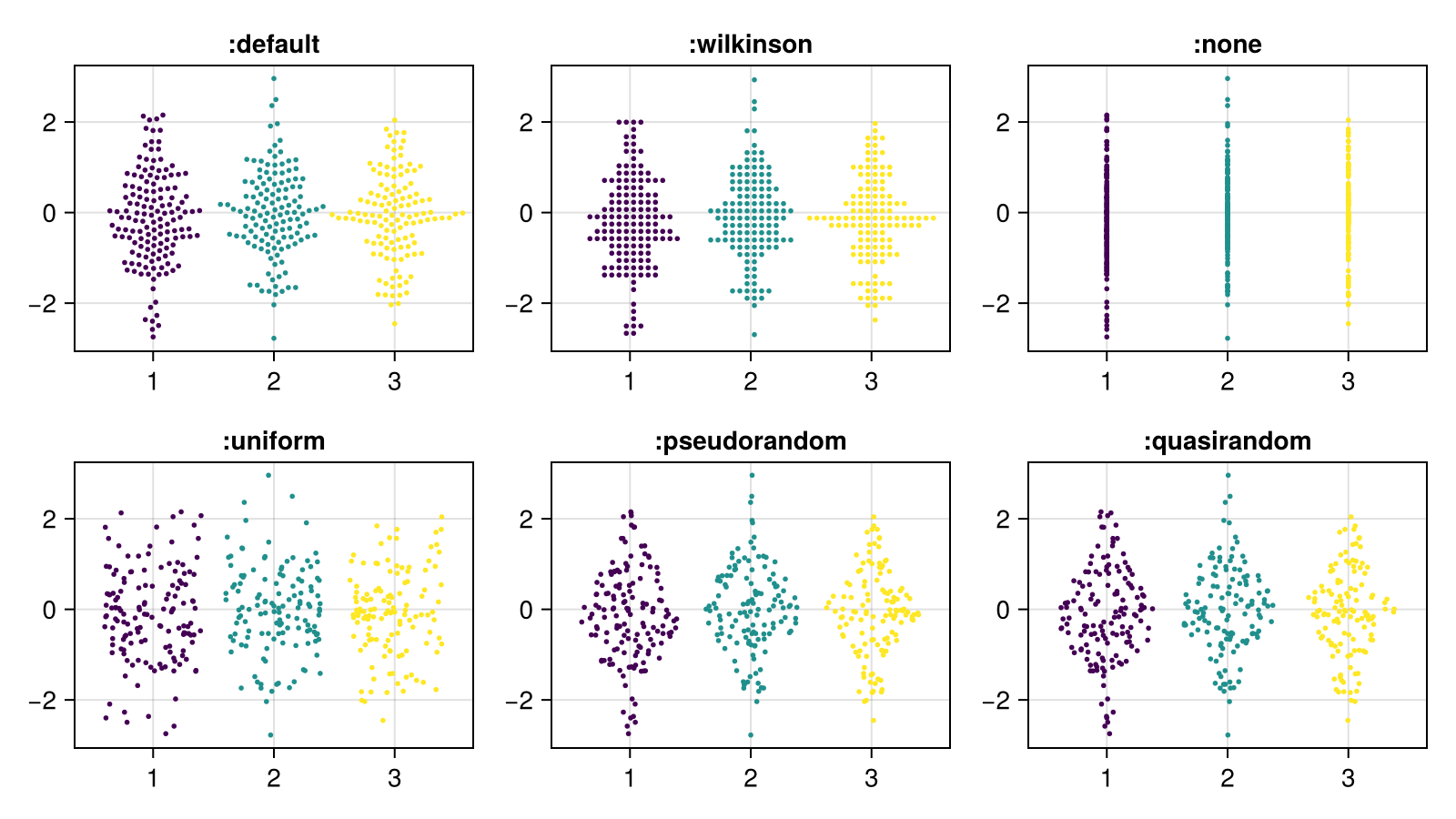

The jitter algorithms respond to a width in data space, similar to how it works for barplot.

using SwarmMakie, CairoMakie

algorithms = [:uniform, :pseudorandom, :quasirandom]
fig = Figure(; size = (800, 450))
xs = rand(1:3, 400); ys = randn(400)

for (j, width) in enumerate([1, 0.5, 0.2])
    for (i, algorithm) in enumerate(algorithms)
        beeswarm(
            fig[i, j], xs, ys;
            color = xs, algorithm, markersize = 4,
            axis = (; title = "$(repr(algorithm)), width = $width"),
            width,
            seed = 123,
        )
    end
end

fig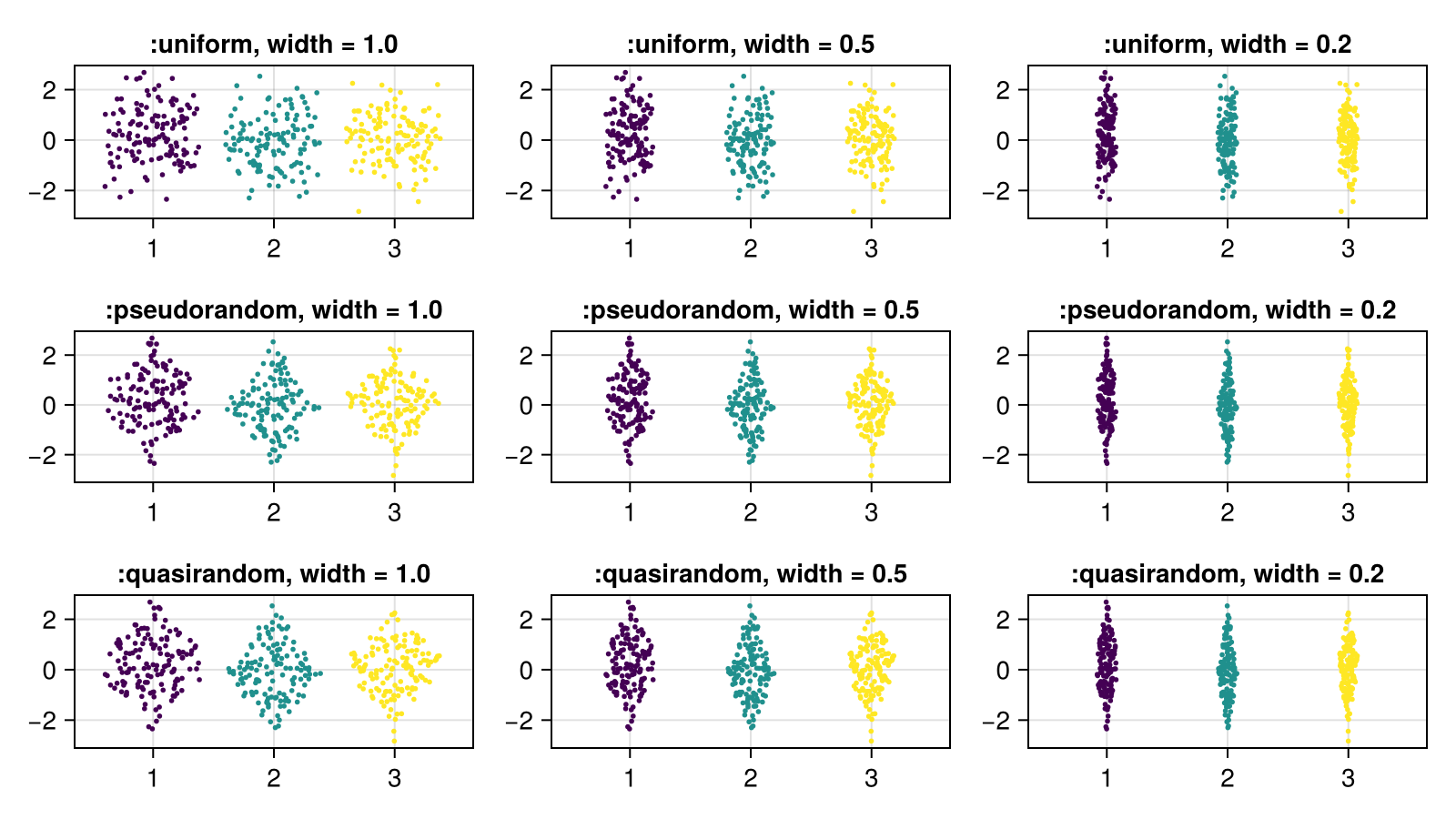

The gap between categories for automatically determined width can be adjusted with the gap parameter.

using SwarmMakie, CairoMakie

fig = Figure()
xs = rand(1:3, 400); ys = randn(400)

for (j, gap) in enumerate([0, 0.3, 0.6])
    beeswarm(
        fig[1, j], xs, ys;
        color = xs, algorithm = :uniform, markersize = 4,
        axis = (; title = "gap = $gap"),
        gap,
        seed = 123,
    )
end

fig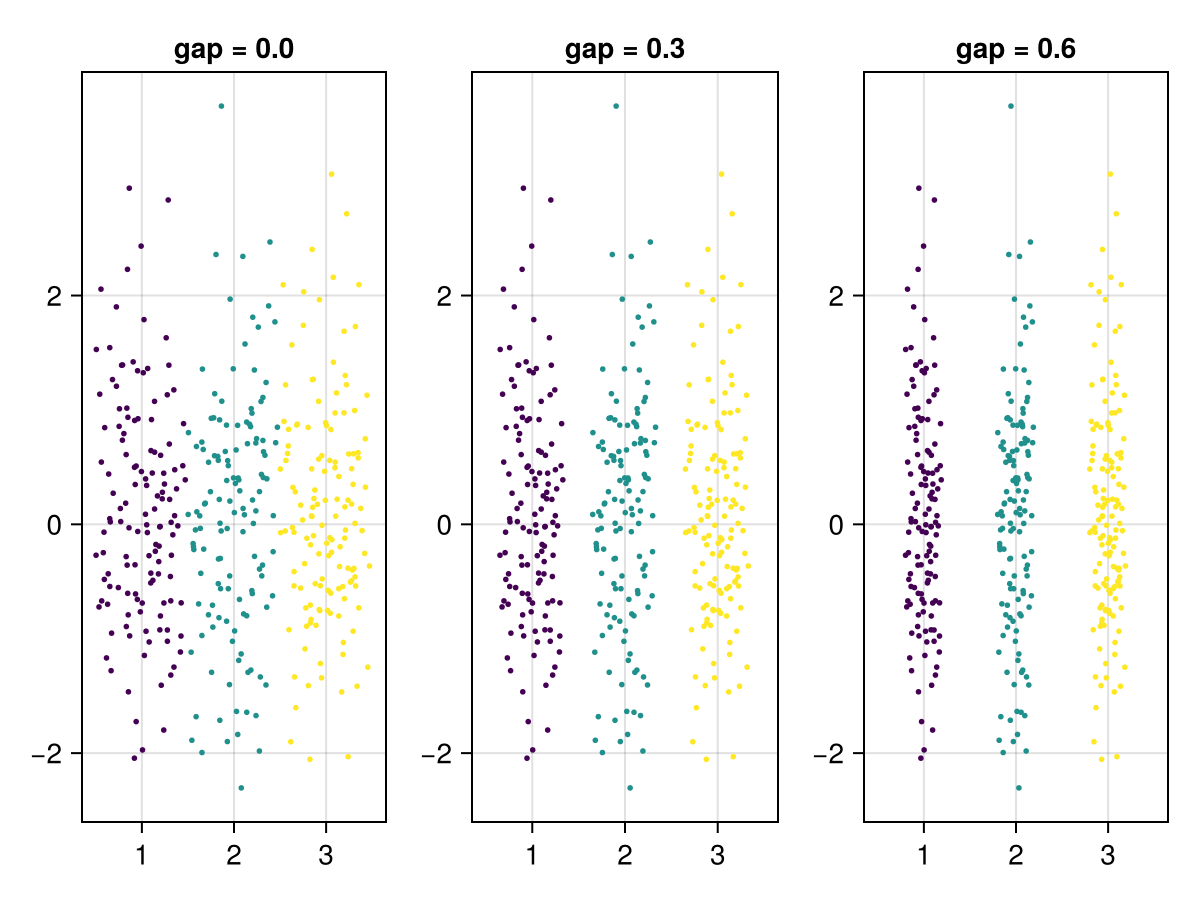

Documentation

SwarmMakie.SimpleBeeswarm Type

SimpleBeeswarm()

A simple beeswarm implementation, that minimizes overlaps. This is the default algorithm used in beeswarm.

This algorithm dodges in x but preserves the exact y coordinate of each point. If you want a more organized appearance and don't need to preserve the exact y coordinates, you can try WilkinsonBeeswarm.

source

SwarmMakie.WilkinsonBeeswarm Type

WilkinsonBeeswarm()

A beeswarm algorithm that implements Leland Wilkinson's original dot-hist algorithm.

This is essentially a histogram with dots, where all dots are binned in the y (non-categorical) direction, and then dodged in the x (categorical) direction.

Original y-coordinates are not preserved, and if you want that try SimpleBeeswarm instead.

source

SwarmMakie.NoBeeswarm Type

A simple no-op algorithm, which causes the scatter plot to be drawn as if you called scatter and not beeswarm.

source

SwarmMakie.UniformJitter Type

UniformJitter()

A jitter algorithm that uses a uniform distribution to create the jitter.

source

SwarmMakie.PseudorandomJitter Type

PseudorandomJitter()

A jitter algorithm that uses a pseudorandom distribution to create the jitter. A pseudorandom distribution is a uniform distribution weighted by the PDF of the data.

source

SwarmMakie.QuasirandomJitter Type

QuasirandomJitter()

A jitter algorithm that uses a quasirandom (van der Corput) distribution weighted by the data's pdf to jitter the data points.

source

We also welcome any new algorithms you may have in mind. Just open a PR!

Adding a new algorithm

In order to add a new algorithm, you must simply define a struct which subtypes SwarmMakie.BeeswarmAlgorithm.

There must also be a corresponding dispatch on SwarmMakie.calculate!(buffer, alg, positions, markersize) which loads the new positions calculated in pixel space into buffer. Note that buffer must be modified here.

See the Wilkinson source page for a deep dive into how to write a beeswarm algorithm!